The algorithms behind the procedural generation of system data
The Data on System screen is, under the hood, a work of mathematical art. Every bit of data on that screen is procedurally generated from the system seeds, specifically from parts of s0_hi, s1_hi and s1_lo. This enables the game to produce system data like the following, all from three 16-bit numbers:
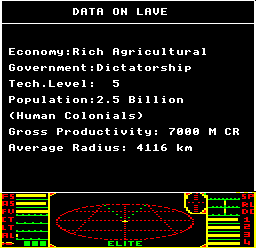
For more details on the system seeds see the deep dive on galaxy and system seeds, but given a set of seeds, let's see how we can generate the data shown in the Data on System screen.
Summary
-------
The following bits of data are generated in routine TT24 and are stored in locations QQ3 to QQ7:
QQ3 = economy (0-7) QQ4 = government (0-7) QQ5 = technology level (0-14) QQ6 = population * 10 (1-71) QQ7 = productivity (96-62480)
The species type and average radius aren't stored anywhere, but are generated on-the-fly in routine TT25 when displaying the system data.
Let's look at how these bits of data are all generated.
Government
----------
The government is given by a 3-bit value, taken from bits 3-5 of s1_lo. This value determine the type of government as follows:
0 = Anarchy 1 = Feudal 2 = Multi-government 3 = Dictatorship 4 = Communist 5 = Confederacy 6 = Democracy 7 = Corporate State
The highest government value is 7 and the lowest is 0.
Economy
-------
The economy is given by a 3-bit value, taken from bits 0-2 of s0_hi. This value determine the prosperity of the economy:
0 or 5 = %000 or %101 = Rich 1 or 6 = %001 or %110 = Average 2 or 7 = %010 or %111 = Poor 3 or 4 = %011 or %100 = Mainly
while bit 2 determines the type of economy:
bit 2 = %0 = Industrial bit 2 = %1 = Agricultural
Putting these two together, we get:
0 = Rich Industrial 1 = Average Industrial 2 = Poor Industrial 3 = Mainly Industrial 4 = Mainly Agricultural 5 = Rich Agricultural 6 = Average Agricultural 7 = Poor Agricultural
If the government is an anarchy or feudal state, we need to fix the economy so it can't be rich (as that wouldn't make sense). We do this by setting bit 1 of the economy value, giving possible values of %010, %011, %110, %111. Looking at the prosperity list above, we can see this forces the economy to be poor, mainly, average, or poor respectively, so there's now a 50% chance of the system being poor, a 25% chance of it being average, and a 25% chance of it being "Mainly Agricultural" or "Mainly Industrial".
The highest economy value is 7 and the lowest is 0.
Technology level
----------------
The tech level is calculated as follows:
flipped_economy + (s1_hi AND %11) + (government / 2)
where flipped_economy is the economy value with its bits inverted (keeping it as a 3-bit value, so if the economy is %001, flipped_economy is %110). The division is done using LSR and the addition uses ADC, so this rounds up the division for odd-numbered government types.
Flipping the three economy bits gives the following spread of numbers:
7 or 2 = %111 or %010 = Rich 6 or 1 = %110 or %001 = Average 5 or 0 = %101 or %000 = Poor 4 or 3 = %100 or %011 = Mainly
This, on average, gives a higher number to rich states compared with poor states, as well as giving higher values to industrial economies compared to agricultural, all of which makes a reasonable basis for a measurement of technology level.
The highest tech level is 7 + 3 + (7 / 2) = 14 (when rounded up) and the lowest is 0. When shown on-screen by the TT25 routine, this value is incremented to give a tech level range of 1 to 15.
Incidentally, the planet's type depends on its tech level. If bit 1 of the planet's tech level is set then the planet has a crater, otherwise it has a meridian and an equator. This means that planets with tech level ending in %10 or %11 will have craters, so that's 2, 3, 6, 7, 10, 11 or 14. When shown on-screen, this means that planets with tech levels of 3, 4, 7, 8, 11, 12 or 15 will have craters, while tech levels 1, 2, 5, 6, 9, 10, 13 and 14 will have meridians and equators.
Population
----------
The population is calculated as follows:
(tech level * 4) + economy + government + 1
This means that systems with higher tech levels, better economies and more stable governments have higher populations, with the tech level having the most influence. The number stored is actually the population * 10 (in billions), so we can display it to one decimal place by calling the pr2 subroutine (so if the population value is 52, it means 5.2 billion).
The highest population is 14 * 4 + 7 + 7 + 1 = 71 (7.1 billion) and the lowest is 1 (0.1 billion).
Productivity
------------
The productivity is calculated as follows:
(flipped_economy + 3) * (government + 4) * population * 8
Productivity is measured in millions of credits, so a productivity of 23740 would be displayed as "23740 M CR".
The highest productivity is 10 * 11 * 71 * 8 = 62480, while the lowest is 3 * 4 * 1 * 8 = 96 (so the range is between 96 and 62480 million credits).
Species type
------------
The species type is either Human Colonials, or it's an alien species that consists of up to three adjectives and a species name (so you can get anything from "Rodents" and "Fierce Frogs" to "Black Fat Felines" and "Small Yellow Bony Lobsters").
As with the rest of the system data, the species is built from various bits in the seeds. Specifically, all the bits in s2_hi are used, along with bits 0-2 of s0_hi and s1_hi, and bit 7 of s2_lo.
First, we check bit 7 of s2_lo. If it is clear, print "Human Colonials" and stop, otherwise this is an alien species, so we move onto the following steps. (In the following steps, the potential range of the calculated value of A is 0-7, and if a match isn't made, nothing is printed for that step.)
- Set A = bits 2-4 of s2_hi
- If A = 0, print "Large "
- If A = 1, print "Fierce "
- If A = 2, print "Small "
- Set A = bits 5-7 of s2_hi
- If A = 0, print "Green "
- If A = 1, print "Red "
- If A = 2, print "Yellow "
- If A = 3, print "Blue "
- If A = 4, print "Black "
- If A = 5, print "Harmless "
- Set A = bits 0-2 of (s0_hi EOR s1_hi)
- If A = 0, print "Slimy "
- If A = 1, print "Bug-Eyed "
- If A = 2, print "Horned "
- If A = 3, print "Bony "
- If A = 4, print "Fat "
- If A = 5, print "Furry "
- Add bits 0-1 of s2_hi to A from step 3, and take bits 0-2 of the result
- If A = 0, print "Rodents "
- If A = 1, print "Frogs "
- If A = 2, print "Lizards "
- If A = 3, print "Lobsters "
- If A = 4, print "Birds "
- If A = 5, print "Humanoids "
- If A = 6, print "Felines "
- If A = 7, print "Insects"
So if we print an adjective at step 3, then the only options for the species name are from A to A + 3 (because we add a 2-bit number) in step 4. So only certain combinations are possible:
- Only rodents, frogs, lizards and lobsters can be slimy
- Only frogs, lizards, lobsters and birds can be bug-eyed
- Only lizards, lobsters, birds and humanoids can be horned
- Only lobsters, birds, humanoids and felines can be bony
- Only birds, humanoids, felines and insects can be fat
- Only humanoids, felines, insects and rodents can be furry
So however hard you look, you will never find slimy humanoids, bony insects, fat rodents or furry frogs, which is probably for the best.
Average radius
--------------
The average radius is calculated as follows:
((s2_hi AND %1111) + 11) * 256 + s1_hi
The highest average radius is (15 + 11) * 256 + 255 = 6911 km, and the lowest is 11 * 256 = 2816 km.